![]()
Sestito Engineering Research Group
We are a research group at Valparaiso University. Our goal is to develop computational tools and models and apply these to engineering applications.
![]()
We are a research group at Valparaiso University. Our goal is to develop computational tools and models and apply these to engineering applications.
Optimization is the method of optimizing a set of parameters, or input variables, such that a set of objectives, or output variables, are minimized (or maximized). In its simplest form, single objective optimization with one parameter can be represented as \(\min_{x} f(x)\). Our goal is then to find the value of \(x\) which minimizes \(f(x)\). If instead we wish to maximize \(f(x)\), we can just minimize \(-f(x)\). This is rather trivial to accomplish but becomes much more difficult as the number of parameters and objectives increase.

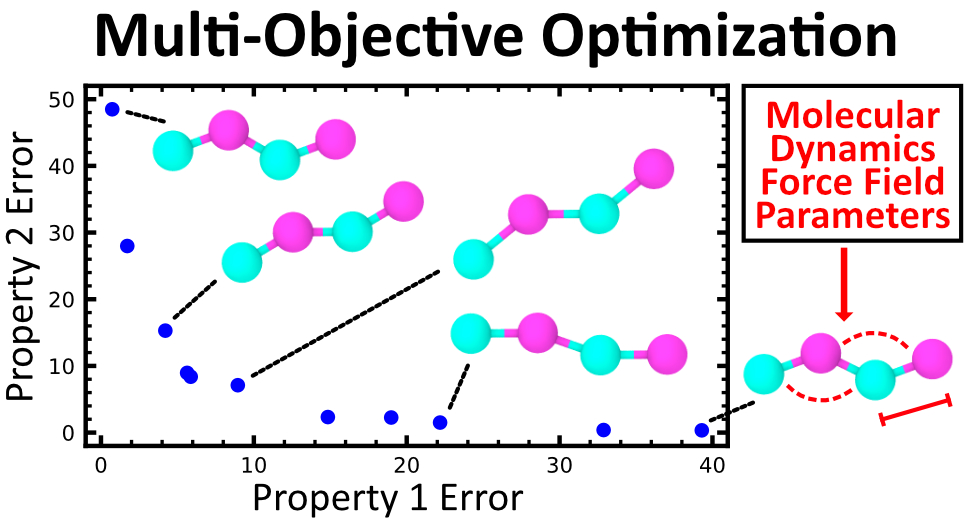
Multi-objective optimization is when the number of objectives is greater than one. For a set of parameters \(\boldsymbol{x} = (x_1, x_2, ... , x_m),\) the optimization problem can be represented as
where the goal is to minimize all of the objectives by modifying the parameters. In a theoretical sense, the ideal soltuion would be an \(\boldsymbol{x}\) which represents the absolute minimum for all objectives simultaneously. However, in a more traditional sense, selecting an \(\boldsymbol{x}\) which minimizes one objective does not minimize the other objectives. However, there are a set of solutions such that it is impossible to decrease the value of one objective by changing the value of \(\boldsymbol{x}\) without increasing the value of the other objectives. This set of solutions results in what is known as the Pareto front, which is a set of non-dominated solutions that for the minimum front of the objective space. This Pareto front holds the ideal solutions to the optimization problem in which a set of design variables should be selected for the desired minimum objectives.
Now, how does this relate to engineering? When desiging parts your always trying to minimze and maximize attributes. Maybe you wish to minimize manufacturing costs and time while keeping with the original design of your product; you then can adjust the geometric design to minimize these two competing objectives. These optimization problems are all around us!
Our goal is to find efficient and effective methods to calculate the pareto front for a large number of parameters and objectives. We also wish to explore optimization engineering problems and apply optimization methods to solve these engineering problems.
There is always interest in developing more efficient high-parameter and high-objective space optimization methods. Sometimes, we even try to push the limits into how many objectives can we optimize for? Projects in this lab include looking into new and exciting optimization methods that can be applied to optimization problems! Students will work to investigate and develop these methods!
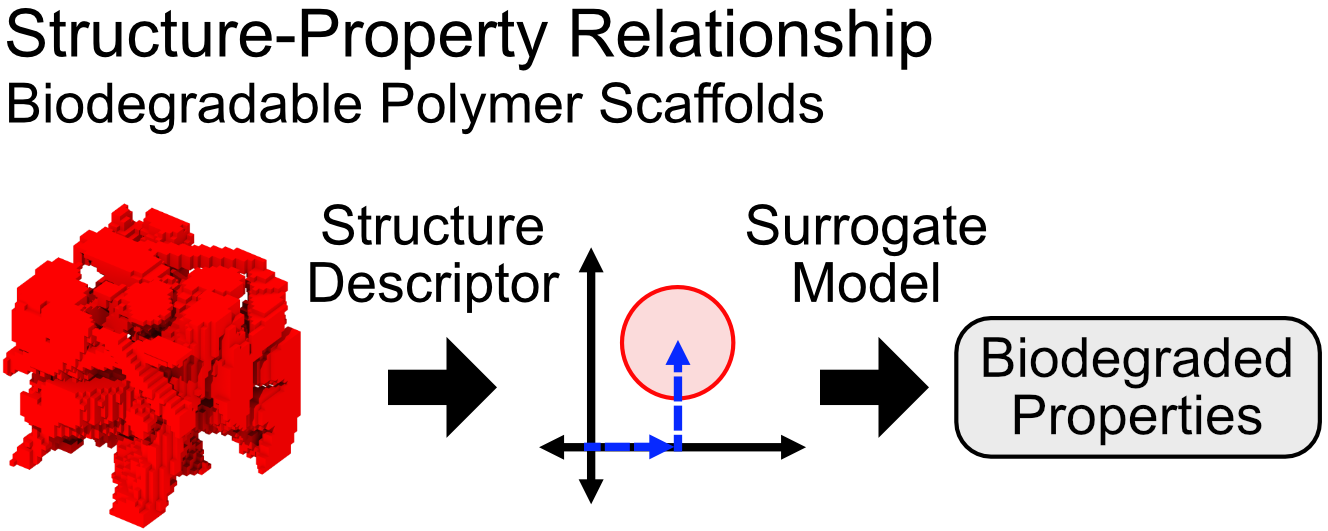
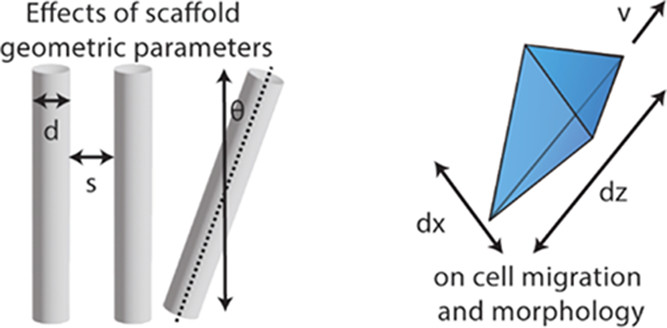
Though, we have looked into some applications of multi-objective optimization, there are always new an exciting engineering problems optimization can be applied to! Currently we are looking into design optimization problems for drone landing gear design and 3D printing optimization. We are always looking into new and exciting applications!
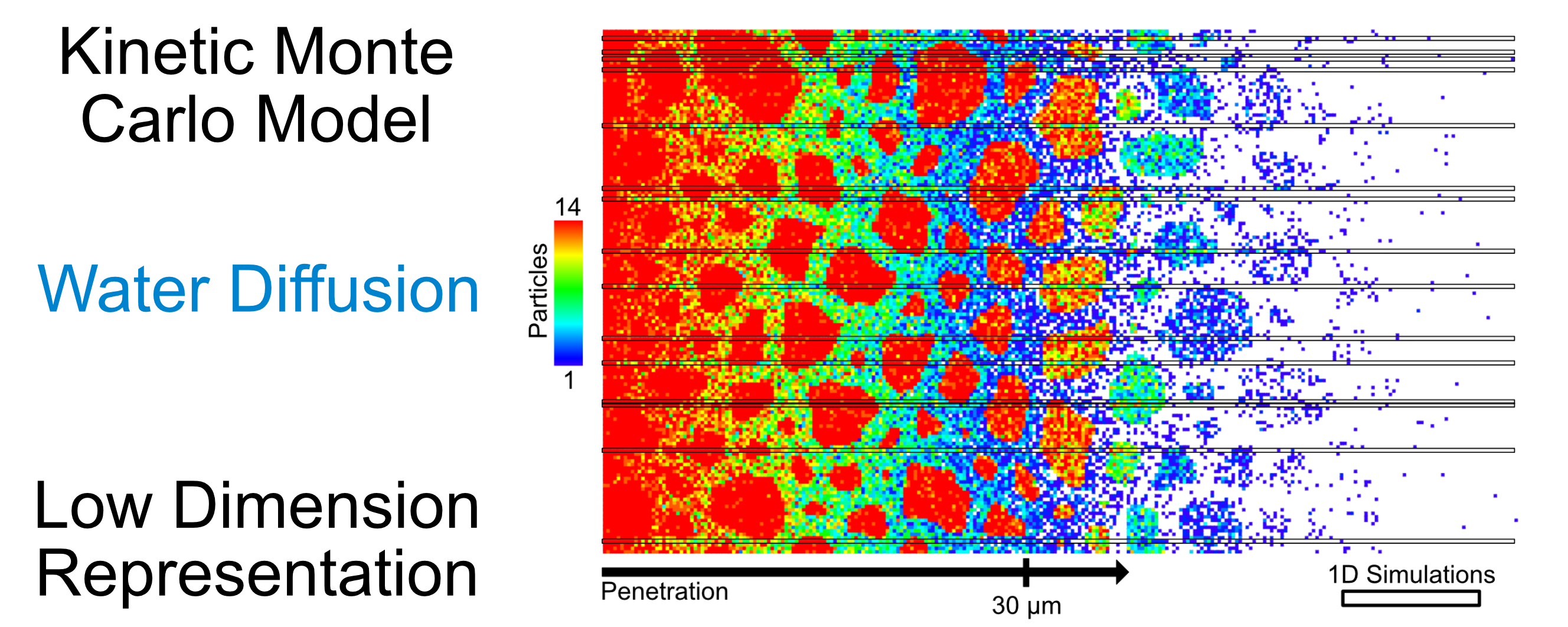
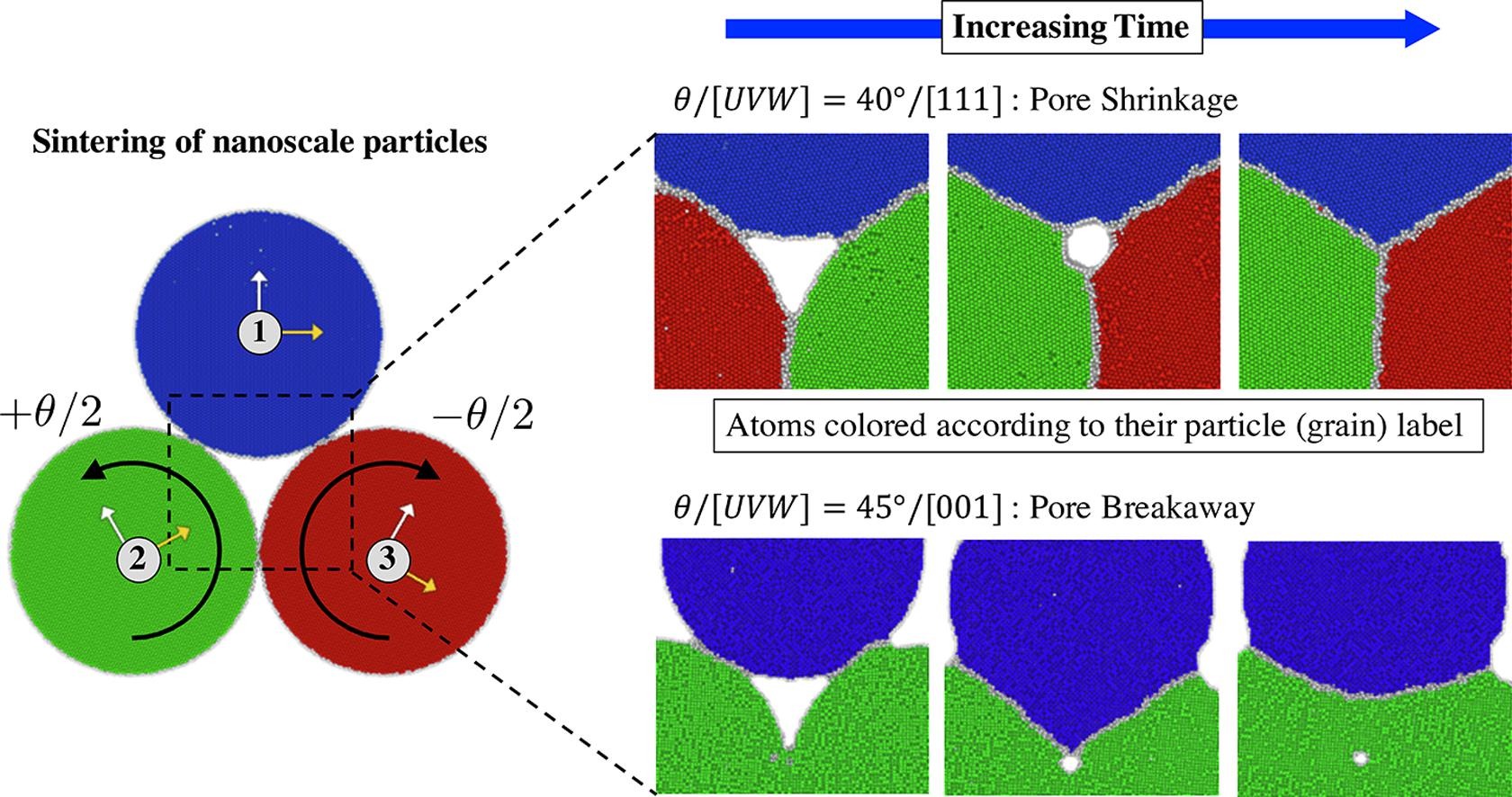
In our lab, we utilize several multiscale modeling techniques to be able to analyze systems. In this lab we work with molecular dynamics, finite element analysis, kinetic Monte Carlo, and more!
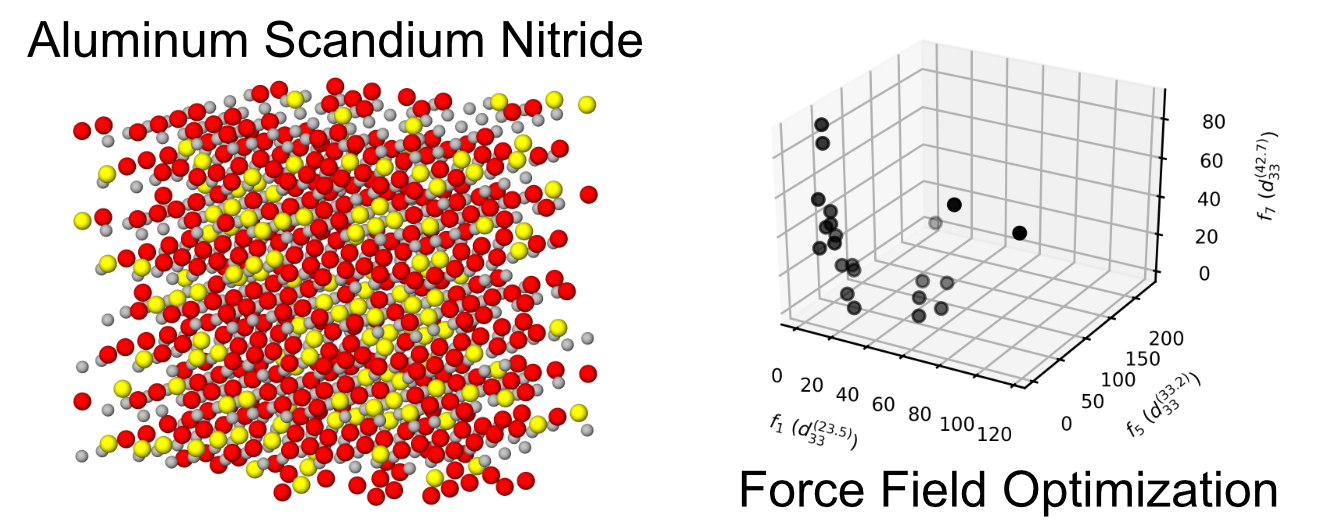
In molecular dynamics simulations, each particle, which can be an individual atom or a group of atoms, is modeled where the position and velocity of each particle is tracked. The positions of the atoms are deterimend by the simulations “Force Field”, which is the information that models the energy of each particle. So, to be able to perform these molecular dynamics simulations, we need force fields that accurately represent the system we are trying to model.
To generate these molecular dynamics force fields, we use optimization to create force fields which acccurately represent the system we wish to model.
If you are an undergraduate at Valpo in engineering interested in research, there are projects in some of the following areas!
Valparaiso University
Fundamentals and principles of mechanical vibration. Mathematical formulation of the equations of motion for single and multi-degree of freedom systems. Analysis of natural frequency, damped natural frequency, free and forced vibration of mechanical systems
Valparaiso University
This laboratory will introduce students to a variety of mechatronic components including microprocessors, PLCs, actuators, sensors, and robotics and allow students to program mechatronics systems to complete a variety of tasks.
Valparaiso University
The objective of this laboratory is to introduce mechanical engineering students to electric machines, mechanical vibrations, automatic control, and ABB industrial robot. This laboratory has a total of seven experiments (three in Vibrations, three in Automatic Control, and one in robotics).
Valparaiso University
The objective of this course is to provide the students with the basic principles of the materials science and engineering. Students will understand the structure of solids (including metals, ceramics, polymer and composite), imperfection of solids, diffusion, mechanical properties of materials, strengthening mechanisms and phase diagrams. Also, students will be aware that the selection of materials depending upon the physical, mechanical, and thermal properties required by the conditions associated with the engineering problems. These properties are controlled and affected by the composition, loading condition, and history (method of fabrication and/or environment) of the materials.
Valparaiso University
Aspects of manufacturing that are not included in a traditional introduction manufacturing course. Topics range from non-traditional manufacturing methods to manufacturing concepts such as computer numeric control, product design management, and test engineering.
Valparaiso University
This course provides instruction on the principles used to understand and model physical systems and introduces methods for building and solving mathematical models of engineering systems. Applications include the modeling of mechanical, thermal, biological and electrical systems and the use of numerical methods and computer programming to solve for the system outputs.
Valparaiso University
Experimental studies design to reinforce theory presented in material science and mechanics of materials. Experiments deal with topics such as mechanical properties of materials, microstructures of materials, strain hardening, and hardness testing.
Valparaiso University
A study of fundamental concepts and physical principles involved in the science of measurement and design of experiments. Experiments involve calibration and testing (both static and dynamic) of primary elements, signal amplifiers, transducers and readout devices. Experimentation utilizes laboratory and industrial instruments.Extensive use is made of computer data acquisition and analysis. A Writing in the Discipline course.
Valparaiso University
Graphical and analytical approaches to kinematic analysis and synthesis of linkages, gears, and cams. Linkage topics include displacement, velocity, and acceleration analysis along with type, number, and dimensional synthesis. Fundamentals of gears and gear trains are investigated. Cam sizing and application of motion programs to cam design are considered.
Valparaiso University
The application of theoretical and experimental engineering concepts in the analysis and design of an engineering system. Students form teams to plan and organize a multidisciplinary project. Projects are built, tested, documented, and reported.
Georgia Institute of Technology
An introduction to numerical methods for the solution of mechanical engineering problems. Topics include: sources of errors in computing, mathematical bases of numerical methods, and implementation of numerical techniques using MATLAB.